


Music, like language, heavily employs context to create shared information. Adrian DiMatteo examines "intonation" and specific key tones in music that, depending on which one you subscribe to, will bring respective harmony to your musical conversations and understanding.
What does it mean to be “in tune”? Picture that moment when a tone-deaf singer gets on stage at the karaoke open-mic. If you know how the song is supposed to sound, it’s all the more obvious when someone misses the mark. But why are the notes we hear different from the notes we expect to hear? The concept of musical intonation is as ancient as musical instruments themselves. A mammoth-ivory flute dating back more than 40,000 years shows that human beings have been implementing musical notes since prehistoric times. Since then humanity has designed an astounding array of instruments made of wood, metal, animal parts, nylon, carbon fiber, and other materials. Depending on their size and construction, different instruments require different tunings.
In order to understand musical tuning, we first need to understand musical notes. A note refers to a specific, stable “pitch” or “frequency.” The same way colors are identified based on their electromagnetic frequencies (light), musical notes are given names according to their sonic frequencies. These frequencies are measured in Hertz. For instance, the note A 440 Hz refers to an oscillation that occurs 440 times per second, producing the note we call “A”. In other cultures, different names are used, but the underlying principle is the same.
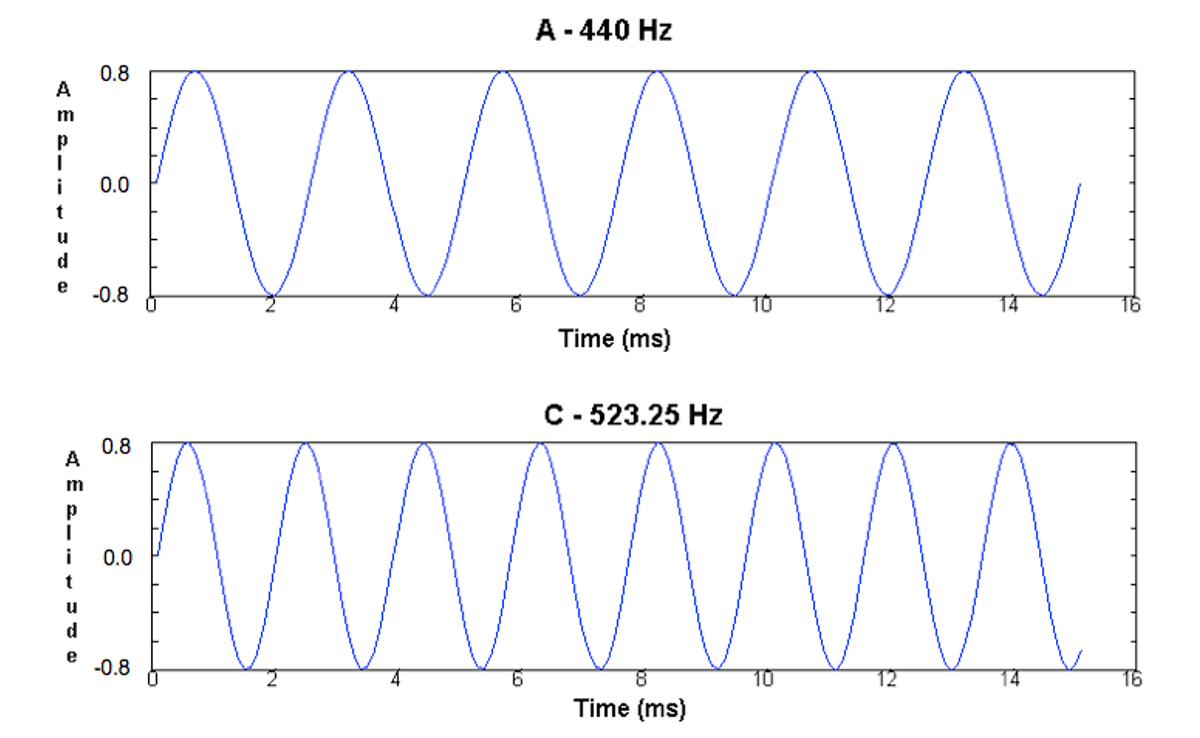
Diagram of Sine Waves Representing A 440 Hz and C 532.25 Hz
The International Organization for Standardization is responsible for establishing the technical definition of the note “A”. They write: “The note A in the treble stave...shall be 440 Hz.” According to this standard, any frequency that is more than 0,5 Hz above or below 440 Hz is considered to be “sharp” or “flat”, respectively. In other words — out of tune.
In a sense, these definitions are arbitrary, the same way we assign names to animals and objects which vary by language. We could have defined “A” as 400 Hz, but we didn’t. In fact, the current tuning standard did not exist prior to the American Standards Association formally recommending it in 1936, and to this day it is not ubiquitously observed. There are many controversies surrounding this standardization, including conspiracy theories which claim that Nazi’s imposed it in order to cause psychophysiological angst, but these rumors have been largely debunked.
Opponents of 440 argue that A 432 Hz is more harmonious for organic systems, pointing to various natural phenomena in support of their view. For instance, the diameter of the moon is roughly 2,160 miles (five times 432). The orbital precession of the equinoxes takes 25,920 years (60 times 432). There are 43,200 seconds in 12 hours (100 times 432). The cross-relationships between these numbers play heavily into base 60 mathematics, and thus geometry and the platonic solids (triangle = 180°, tetrahedron = 720°, square = 320°, cube = 2160°, octahedron = 1440°). However, since numerical systems vary (as in metric vs imperial measurement), these connections are only subjectively relevant.
Proponents of Solfeggio Frequencies use numerology to select specific tones that are related to 3, 6 and 9. The Solfeggio frequencies are 147 Hz, 285 Hz, 396 Hz, 417 Hz, 528 Hz, 639 Hz, 741 Hz, 852 Hz and 963 Hz. This rather esoteric approach assumes that numbers have some intrinsic power of their own, and can therefore be projected through sound vibration to produce healing effects. However, these frequencies do not produce objectively “better” music, and some consider numerology to be pseudo-scientific.
Another popular “healing frequency” is known as the Schumann Resonance. The Schumann Resonance refers to an electromagnetic frequency that resonates between the Earth’s surface and the ionosphere. These two geophysical boundaries act as a “waveguide” for the resonance produced by photons (sustained by lightning) which become trapped in the atmosphere. The fundamental wavelength of the Schumann Resonance (7.38 Hz) is equal to the circumference of the Earth, and is sometimes referred to as the “heartbeat of the earth.” Subsequently, researchers using EEG tests have confirmed that frequencies related to the Schumann Resonance are similar to Delta, Theta, Alpha, Beta and Gamma brain waves associated with deep sleep, relaxation and concentration.
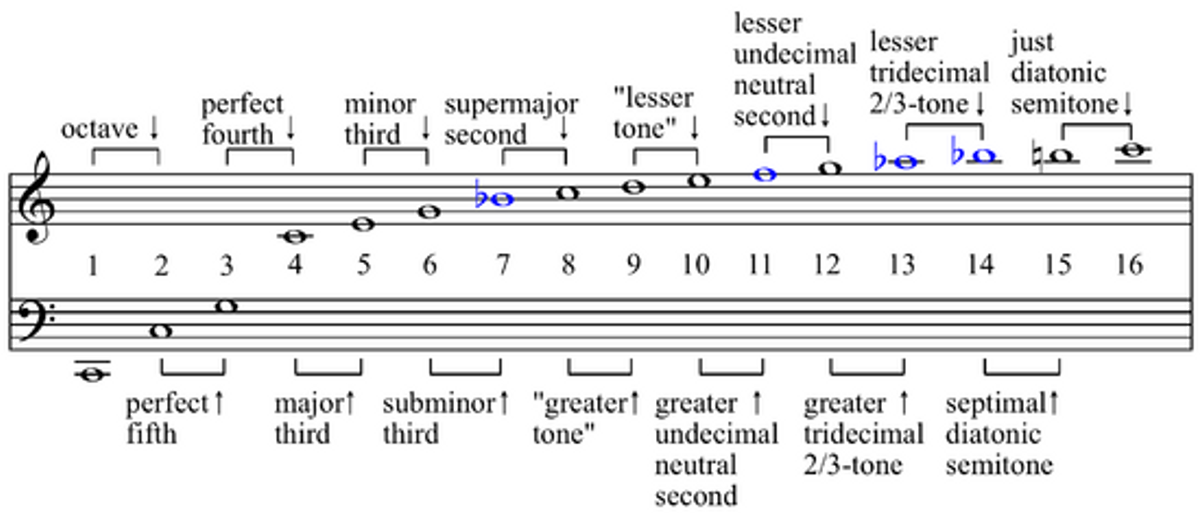
Like ripples in a pond, musical notes are complex. The properties of resonance produce many tones, like a stone dropped in water produces many ripples. A harmonic or overtone is a frequency that exists in mathematical relationship to its fundamental (the primary note we hear when a tone is played). For instance, A 440 Hz produces an overtone one octave higher at A 880 Hz. This 2:1 ratio was famously observed by Pythagoras, who is credited as having first noted that “a string exactly half the length of another will play a pitch that is exactly an octave higher when struck or plucked.” Pythagorean Tuning is based on perfect ratios, such as the octave (2:1) and the fifth (3:2). Many ancient instruments were constructed using these proportions. Singing in unison (1:1) is the most intuitive, followed by the octave when, for instance, a man with a low-pitched voice sings the same melody as a woman or child with a higher-pitched voice.
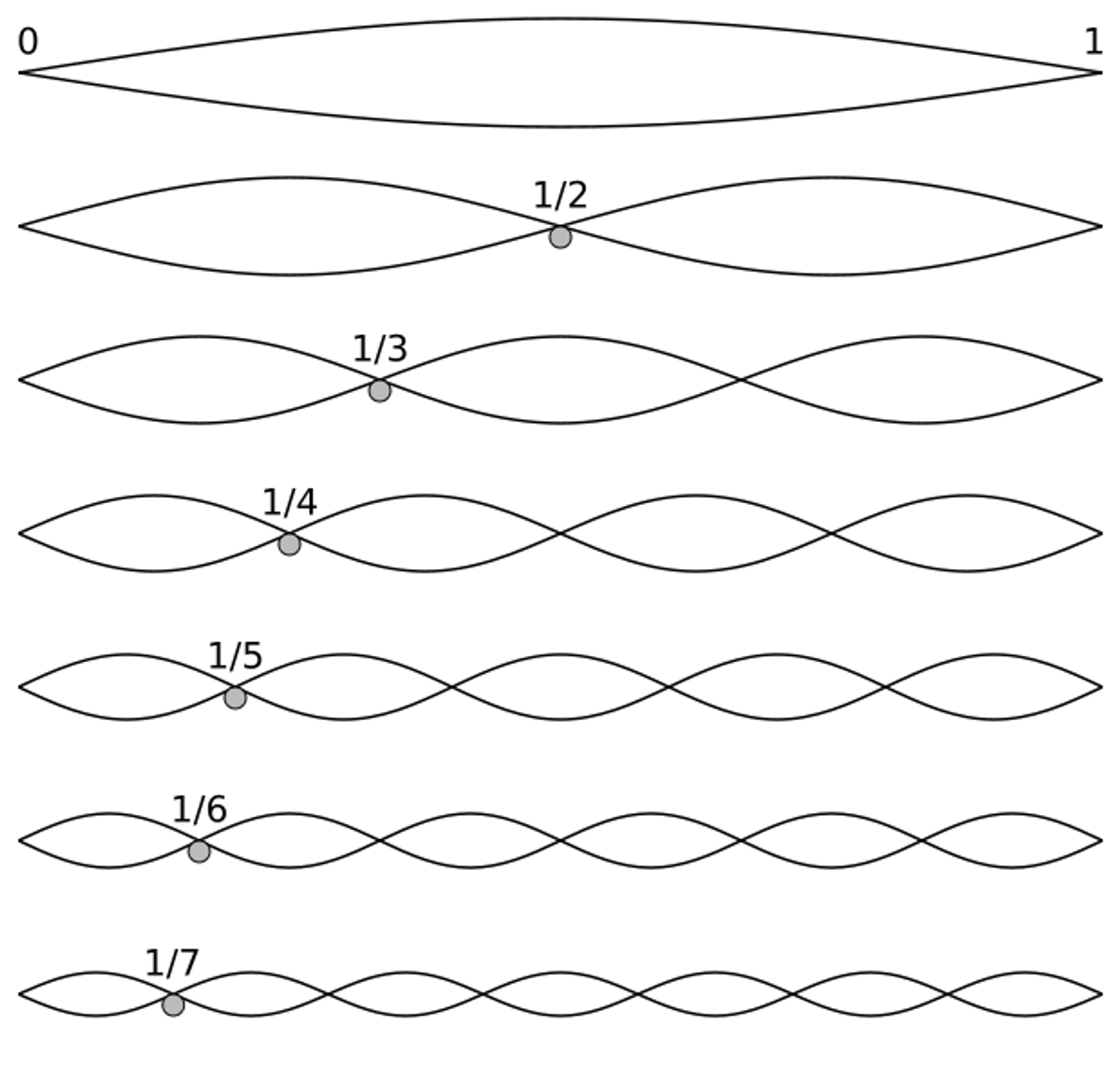
Frequency Ratios of Vibrating Strings
Modern tuning systems are far more complex. Whereas just intonation (described above) uses whole-number ratios to calculate the relationship between musical notes, 12-tone equal temperament uses a logarithmic formula to divide an octave in 12 equal parts. This system produces the 12 notes used in most recorded music today (picture the 7 white keys and 5 black keys of the piano). These 12 notes are essentially the alphabet of music. The same way 26 letters of the English alphabet are used to create countless books, the 12 musical notes are recombined to create countless melodies. By evenly dividing notes, rather than basing their relationships on whole-number ratios, all 12 can be used in various combinations without producing inconsistent intervals.
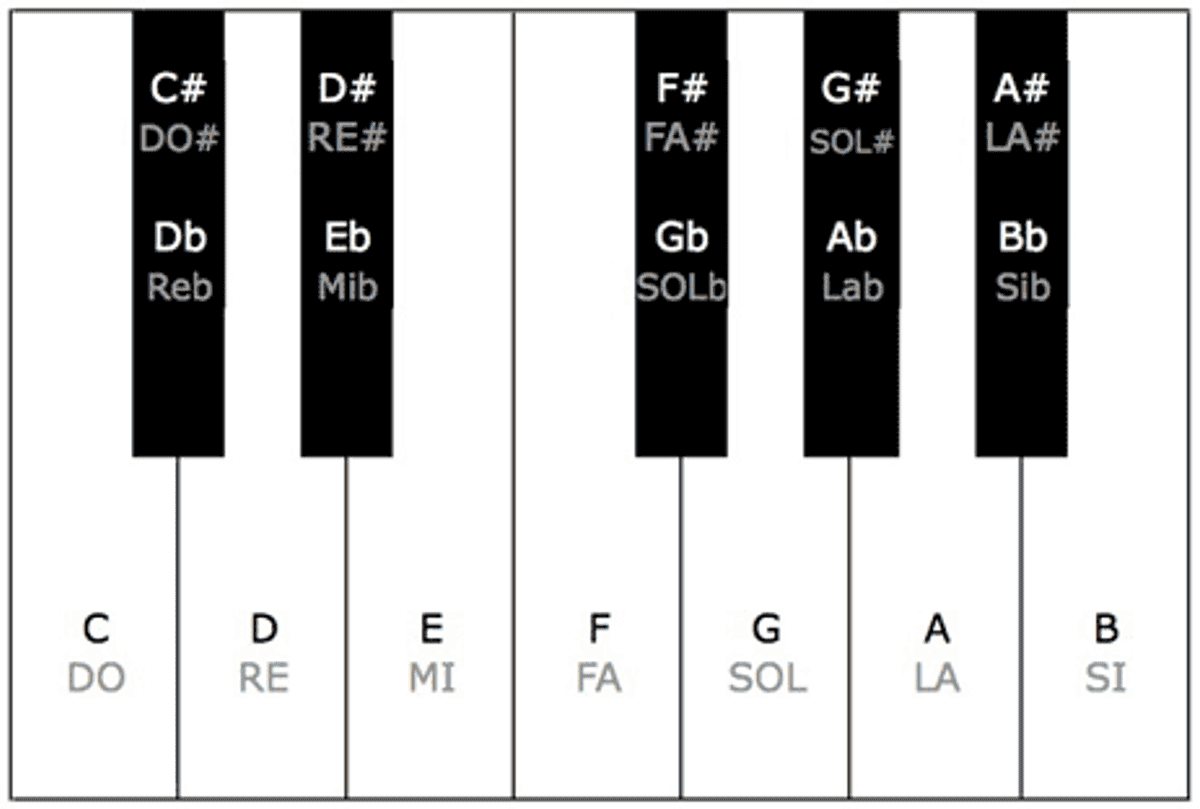
Diagram of One Octave on a Piano Keyboard
The real mystery of musical intonation is why, when and how we came to hear music the way we do as a human race. The similarities of ancient and extant tribal music from around the world are striking. For instance, the pentatonic scale (greek for “five tones”) is used by virtually every autochthonous tradition. It can be heard in the Amazon, throughout Africa, amongst the aboriginal people of Australia, indigenous tribes of the Americas, and across Asia. The same scale is found throughout rock, blues, jazz, funk, hip-hop and soul music.
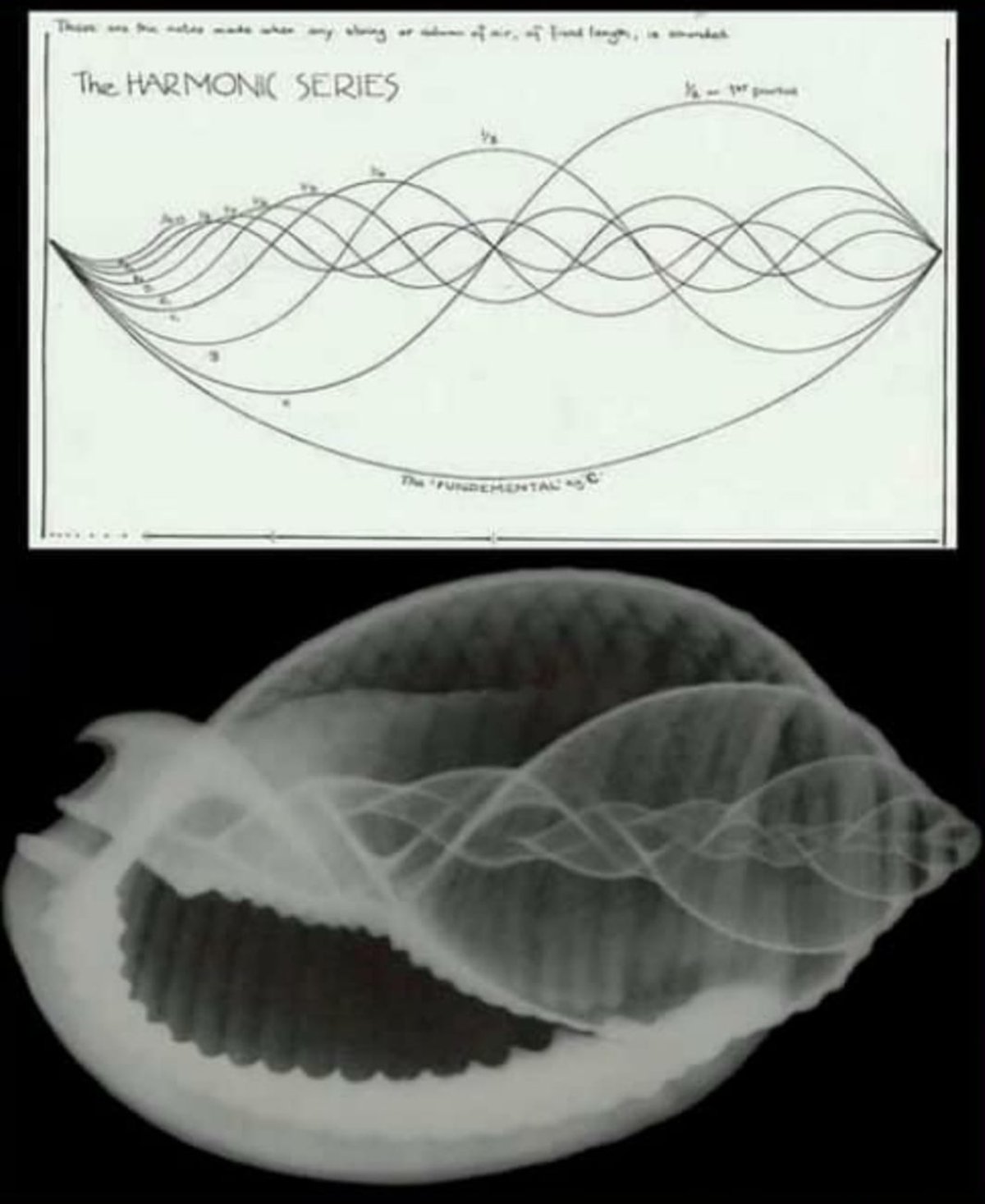
Perhaps the best explanation for this phenomenon is that the notes of the pentatonic scale sympathetically resonate whenever a note is played. Have you ever sang in the shower and felt like your voice was amplified? This is due to the fact that the room itself resonates like the hollow body of a guitar, causing certain notes to project more. In music, the harmonic or overtone series describes which frequencies emerge from a fundamental tone. Like sunlight split through a prism, a note can be split into an array of sounds, revealing the overtones.
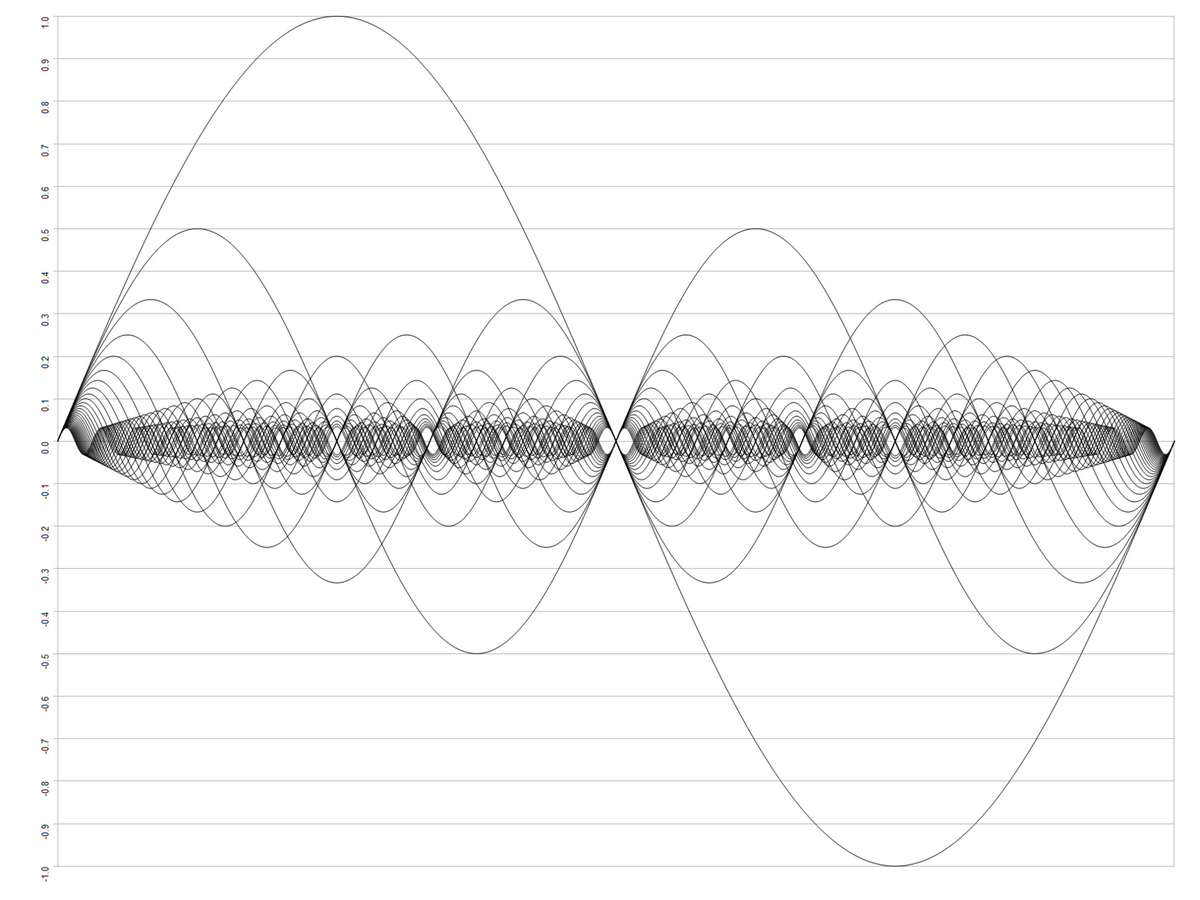
Harmonic or Overtone Series
The distance from one note to another is known as an interval. Since there are 12 notes, there are 12 intervals, just like inches on a ruler. Musical scales are constructed using these intervals. The same way a square or triangle has a formula describing its construction, musical scales follow formulas that define their structure.
One of the most common musical scales is the Major scale. You probably know it from the “Sound of Music,” where Julie Andrews teaches a group of children music theory through song to memorize Do - Re - Mi - Fa - So - La - Ti/Si - (Do). This seven-note scale provides the underlying architecture for literally millions of compositions. The syllables chosen for the scale have been in use for hundreds of years. Originally, “Do” was “Ut”, and the entire series was based on the “Ut Queant Laxis” or “Hymn to St. John the Baptist”:
Ut queant laxīs
resonāre fibrīs
Mīra gestōrum
famulī tuōrum,
Solve pollūtī
labiī reātum,
Sāncte Iohannēs.
It translates as: “So that your servants may, with loosened voices, resound the wonders of your deeds, clean the guilt from our stained lips, O Saint John.”
The art, science and mathematics of sound and music can be quite complex. Although beauty standards are subjective, the mathematical principles of tuning, once established, are not. Thanks to musical intonation, an orchestra of 50 musicians can cohesively perform a symphony. Whatever system of logic is used, people need to agree on some level in order to communicate musically and produce harmony. Harmony itself means ‘to join’ or ‘bring together.’ Music has the power to unify people. As a musician, I have often found myself in foreign countries where, despite not speaking the language, I was able to communicate with others through music because music is a language. Like the Jackson 5 said, it’s “as simple as Do — Re — Mi, A — B — C, 1 — 2 — 3, baby you and me.”